∵点P（x，y）

∴

OP

=（x，y）

∵

OM

=（1，

1

2

），

ON

=（0，1）

∴

OP

•

OM

=x+

1

2

y，

OP

•

ON

=y

∵0≤

OP

•

ON

≤1，0≤

OP

•

OM

≤1

∴0≤x+

1

2

y≤1，0≤y≤1 

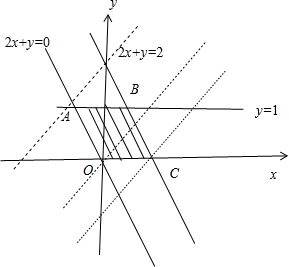
作出该不等式组所确定的平面区域，如图所示的阴影部分，作直线L：y-x=0，然后把直线L向可行域方向平移，

由目标函数Z=y-x可得y=x+Z，则Z为直线y=x+z在y轴的截距，从而可知向上平移是，Z变大，向下平移时，Z变小

到A时Z有最大值，当移到C时Z最小值

由 y=1 2x+y=0   可得A（-

1

2

，1），此时Z最大=y-x=

3

2

即Z的最大值为

3

2

故答案为：

3

2