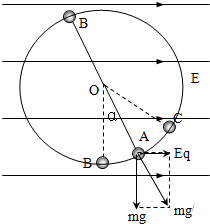
如图所示,一条长为L的绝缘细线一端固定在O点,另一端拴有一个质量为m的带电小球,将它置于场强大小为E的水平方向的匀强电场中,当小球处在细线与竖直方向的夹角为α的A点时处于平衡状态,问:
(1)小球带何种电荷?所带电荷量为多少?
(2)在平衡位置以多大的速度VA释出小球,才能使之在电场中作竖直平面内的完整圆周运动?
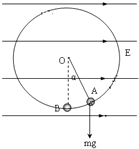
(1)小球受重力mg、电场力Eq、线的拉力T作用,如图可知小球受电场力与电场方向平行,故小球带正电.
根据平衡条件得:
Eq=mgtanα,
解得:q=
;mgtanα E
(2)简化处理,将复合场(重力场和电场)等效为重力场,小球在等效重力场中所受重力为mg′,
由图有:mg′=
,(mg)2+(Eq)2
即g′=
.(mg)2+(Eq)2 m
小球在A点处于平衡状态,若小球在A点以速度VA开始绕O点在竖直平面内作圆周运动,若能通过延长线上的B点(等效最高点)就能做完整的圆周运动,在B点根据向心力公式得:T+mg′=
.mVB2 L
T≥0为临界条件,所以VB≥g′L
又因仅重力、电场力对小球做功,
由动能定理得:-mg′2L=
m1 2
-V 2A
mVB21 2
由以上二式解得:VA≥
=5g′L
=5L (mg)2+(Eq)2 m
.5gL cosα
答:(1)小球带正电荷?所带电荷量为
;mgtanα E
(2)在平衡位置至少以
的速度释出小球,才能使之在电场中作竖直平面内的完整圆周运动.5gL cosα