问题
填空题
设f(x)=ax2+bx,且1≤f(-1)≤2,3≤f(1)≤4,则f(-2)的取值范围是______.
答案
由f (x)=ax2+bx得f(-1)=a-b ①;f(1)=a+b ②
由①+②得2a=[f(1)+f(-1)],
由②-①得2b=[f(1)-f(-1)]
从而f(-2)=4a-2b=2[f (1)+f(-1)]-[f(1)-f(-1)]=3f(-1)+f(1)
∵1≤f(一1)≤2,3≤f(1)≤4
∴3×1+3≤3f(-1)+f(1)≤3×2+4
∴6≤3f(-1)+f(1)≤10
∴f (-2)的取值范围是:6≤f (-2)≤10,即f(-2)的取值范围是[6,10]
故答案为:[6,10]

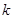 =9.0×l09 N.m2/C2)求:
=9.0×l09 N.m2/C2)求: