变量x、y满足x-4y+3≤03x+5y-25≤0x≥1，（1）求z=2x+y的

问题解答题

变量x、y满足

x-4y+3≤0

3x+5y-25≤0

x≥1

，
（1）求z=2x+y的最大值；
（2）设z=

，求z的最小值；
（3）设z=x²+y²，求z的取值范围；
（4 ）设z=x²+y²+6x-4y+13，求z的取值范围．

答案

由约束条件

x-4y+3≤0

3x+5y-25≤0

x≥1

，

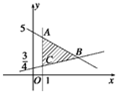
作出（x，y）的可行域如图所示．

由

x=1

3x+5y-25=0

，解得A（1，

）．

由

x=1

x-4y+3=0

，解得C（1，1）．

由

3x+5y-25=0

x-4y+3=0

，解得B（5，2）． …．（4分）

（1）z_max=12…．（7分）

（2）∵z=

∴z的值即是可行域中的点与原点O连线的斜率．

观察图形可知z_min=k_OB=

．…．（10分）

（3）z=x²+y²的几何意义是可行域上的点到原点O的距离的平方．结合图形可知，可行域上的点到原点的距离中，

d_min=OC=，d_max=OB=．∴2≤z≤29…..（13分）

（4）z=x²+y²+6x-4y+13=（x+3）²+（y-2）²的几何意义是可行域上的点到点（-3，2）的距离的平方．结合图形可知，可行域上的点到（-3，2）的距离中，d_min=1-（-3）=4，d_max═8．

∴16≤z≤64…（16分）