问题
填空题
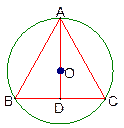
在半径为R的圆内,作内接等腰三角形,当底边上高为_______时它的面积最大.
答案
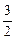 R
R
设圆内接等腰三角形的底边长为2x,高为h,
那么h=AO+BO=R+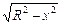 ,解得
,解得
x2=h(2R-h),于是内接三角形的面积为
S=x·h=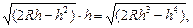
从而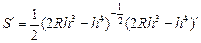
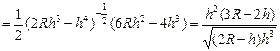
令S′=0,解得h=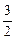 R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
| h | (0,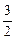 R) R) | 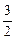 R R | (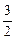 ,2R) ,2R) |
| S′ | + | 0 | - |
| S | 增函数 | 最大值 | 减函数 |
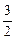 R时,等腰三角形面积最大.
R时,等腰三角形面积最大. 