问题
选择题
在区间[0,1]上任取两个数a,b,则函数f(x)=x2+ax+b2无零点的概率为( )
|
答案
在区间[0,1]上任取两个数a,b,函数f(x)=x2+ax+b2无零点⇔x2+ax+b2=0无实数根,a,b∈[0,1]⇔△=a2-4b2<0,a,b∈[0,1].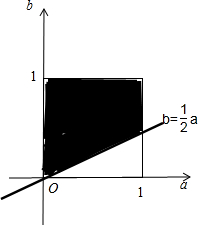
由约束条件
,画出可行域:a,b∈[0,1] a2<4b2
∴函数f(x)=x2+ax+b2无零点的概率P=1-
×1×1 2
=1 2
.3 4
故选C.
