(1) 证明略(2)点A的坐标为(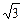，log₈)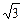

设点A、B的横坐标分别为x₁、x₂,

由题意知： x₁>1,x₂>1,则A、B纵坐标分别为log₈x₁,log₈x₂.

因为A、B在过点O的直线上，

所以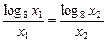,点C、D坐标分别为(x₁,log₂x₁),(x₂,log₂x₂),

由于log₂x₁=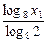=3log₈x₂,

所以OC的斜率： k₁=,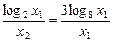

OD的斜率： k₂=，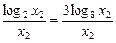

由此可知: k₁=k₂,即O、C、D在同一条直线上.

(2)解: 由BC平行于x轴知：log₂x₁=log₈x₂ 

即 log₂x₁=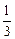log₂x₂,代入x₂log₈x₁=x₁log₈x₂得x₁³log₈x₁=3x₁log₈x₁,

由于x₁>1知log₈x₁≠0,∴x₁³=3x₁.

又x₁>1,∴x₁=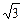,则点A的坐标为(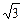，log₈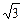).