问题
填空题
已知实数x,y满足(x+2)2+(y-3)2=1,则|3x+4y-26|的最小值为______.
答案
|3x+4y-26|的几何意义是圆上的点到直线3x+4y-26=0的距离减去半径后的5倍,
(即:|3x+4y-26|=5(
-r),(a,b)是圆心坐标,r是圆的半径.)|3a+4b-26| 32+42
就是所以实数x,y满足(x+2)2+(y-3)2=1,则|3x+4y-26|的最小值.
圆的圆心坐标(-2,3),半径是1,
所以圆心到直线的距离为:
=4,|3×(-2)+4×3-26| 5
所以|3x+4y-26|的最小值为5×(4-1)=15.
故答案为:15.

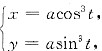 (a>0)绕Ox轴旋转所得旋转曲面的面积为______.
(a>0)绕Ox轴旋转所得旋转曲面的面积为______.