问题
解答题
已知抛物线C1:y=mx2+(2m+1)x+m+1,其中m≠0。
(1)求证:m为任意非零实数时,抛物线C1与x轴总有两个不同的交点;
(2)求抛物线C1与x轴的两个交点的坐标(用含m的代数式表示);
(3)将抛物线C1沿x轴正方向平移一个单位长度得到抛物线C2,则无论m取任何非零实数,C2都经过同一个定点,直接写出这个定点的坐标。
答案
解:(1)证明:∵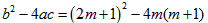 =
=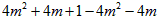 =1>0,
=1>0,
∴一元二次方程mx2+(2m+1)x+m+1=0有两个不相等的实数根,
即:m取任意非零实数,抛物线C1与轴总有两个不同的交点;
(2)∵mx2+(2m+1)x+m+1=0的两个解分别为:x1=-1,x2= ,
,
∴A(-1,0),B(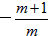 ,0);
,0);
(3)∵抛物线C1与x轴的一个交点的坐标为A(-1,0),
∴将抛物线C1沿x轴正方向平移一个单位长度得到抛物线C2与x轴交点坐标为(0,0),
即无论m取任何非零实数,C2必经过定点(0,0)。
