问题
解答题
已知一元二次方程x2+px+q+1=0的一根为2。
(1)求q关于p的函数关系式;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
(3)设抛物线y=x2+px+q+1与x轴交于A、B两点(A、B不重合),且以AB为直径的圆正好经过该抛物线的顶点,求p,q的值。
答案
解:(1)由题意得22+2p+q+1=0,即q=-2p-5;
(2)∵一元二次方程x2+px+q=0的判别式△=p2-4q,
由(1)得△=p2+4(2p+5)=p2+8p+20=(p+4)2+4>0,
∴一元二次方程x2+px+q=0有两个不相等的实根,
∴抛物线y=x2+px+q与x轴有两个交点;
(3)由题意,x2+px-2p-4=0,
解此方程得x1=2,x2=-p-2 (p≠-4),
∴AB=p+4(p>-4)或AB=-P-4(P<-4),
∵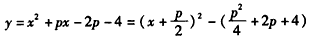
∴顶点坐标是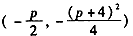 ,
,
∵以AB为直径的圆经过顶点,
∴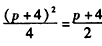 或
或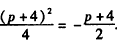 ,
,
解得p=-2或p=-6,
∴P=-2,q=-1或p=-6,q=7。
