问题
解答题
已知关于x的一元二次函数f（x）=ax2-bx+1，分别从集合P和Q中随机取一个数a和b得到数列（a，b）．
（1）若P={x|1≤x≤3，x∈Z}，Q={x|-1≤x≤4，x∈Z}，列举出所有的数对（a，b），并求函数y=f（x）有零点的概率；
（2）若P={x|1≤x≤3，x∈R}，Q={x|-1≤x≤4，x∈R}，求函数y=f（x）在区间[1，+∞）上是增函数的概率．
答案
（1）∵函数y=f（x）有零点，则△=b2-4a≥0即4a≤b2
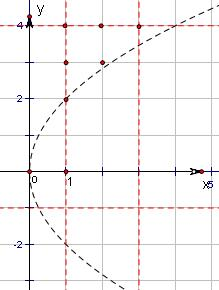
如图，4a≤b2包含6个点：（1，2），（1，3），（1，4），（2，3），（2，4），（3，4），∴事件4a≤b2包含基本事件的个数是6个，而P={x|1≤x≤3，x∈Z}，Q={x|-1≤x≤4，x∈Z}，包含3×6个点，
∴所求事件的概率为
=6 3×6
；1 3
（2）函数f（x）=ax2-bx+1的图象的对称轴为x=
，b 2a
当且仅当b≤2a且a＞0时，
函数f（x）=ax2-bx+1在区是间[1，+∞）上为增函数，
依条件可知试验的全部结果所构成的区域为；
P={x|1≤a≤3，x∈R}，Q={x|-1≤b≤4，x∈R}，
构成所求事件的区域为长方形部分．
而{（a，b）|1≤a≤3，-1≤b≤4，b≤2a且a＞0}包含的区域为图中的阴影部分．
∴所求事件的概率为P=
=S阴影 S长方形
=2×5-
×1×21 2 2×5
．9 10
