问题
选择题
以半径为1的圆内任一点为中点作弦，则弦长超过圆内接等边三角形边长的概率是（ ）
|
答案
由题意可得：符合条件的点必须在内接等边三角形的内切圆内，
理由如下：因为两圆的圆心相同，大圆的半径为1，故内接正三角形的边长为3
故内接等边三角形的内切圆半径为1 2
故=
=S小圆 S大圆
=π(
)21 2 π12 1 4
故选C
搜题请搜索小程序“爱下问搜题”
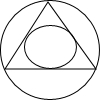
以半径为1的圆内任一点为中点作弦，则弦长超过圆内接等边三角形边长的概率是（ ）
|
由题意可得：符合条件的点必须在内接等边三角形的内切圆内，
理由如下：因为两圆的圆心相同，大圆的半径为1，故内接正三角形的边长为3
故内接等边三角形的内切圆半径为1 2
故=
=S小圆 S大圆
=π(
)21 2 π12 1 4
故选C