问题
解答题
| 在平面直角坐标系xOy中，平面区域W中的点的坐标（x，y）满足x2+y2≤5，从区域W中随机取点M（x，y）． （Ⅰ）若x∈Z，y∈Z，求点M位于第四象限的概率； （Ⅱ）已知直线l：y=-x+b（b＞0）与圆O：x2+y2=5相交所截得的弦长为
|
答案
（Ⅰ）若x∈Z，y∈Z，则点M的个数共有21个，
列举如下：（-2，-1），（-2，0），（-2，1）；（-1，-2），（-1，-1），（-1，0），（-1，1），（-1，2）；（0，-2），（0，-1），（0，0），（0，1），（0，2）；（1，-2），（1，-1），（1，0），（1，1），（1，2）；（2，-1），（2，0），（2，1）．
当点M的坐标为（1，-1），（1，-2），（2，-1）时，点M位于第四象限．
故点M位于第四象限的概率为
．（6分）1 7
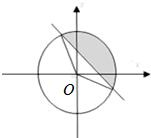（Ⅱ）由已知可知区域W的面积是5π．
因为直线l：y=-x+b与圆O：x2+y2=5的弦长为
，15
如图，可求得扇形的圆心角为
π，2 3
所以扇形的面积为S=
×1 2
π×2 3
×5
=5
π，5 3
则满足y≥-x+b的点M构成的区域的面积为S=
π-5 3
×1 2
×5
×sin5
π=2 3
，20π-15 3 12
所以y≥-x+b的概率为
=20π-15 3 12 5π
．（13分）4π-3 3 12π