问题
解答题
已知函数f(x)=x2 mlnx
(1)若函数f(x)在(,+∞)上是递增的,求实数m的取值范围;
(2)当m=2时,求函数f(x)在[1,e]上的最大值和最小值
答案
(1)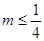 ;(2)
;(2)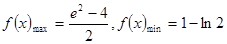 ;
;
题目分析:(1)主要利用函数在区间上的单调递增转化为导数在该区间上恒大于零,然后再把恒成立问题转化为最值来求;(2)利用导数分析函数在区间上的单调性,然后求对应的最值
试题解析:(1)若函数f(x)在(,+∞)上是增函数,
则f′(x)≥0在(,+∞)上恒成立 2分
而f′(x)=x ,即m≤x2在(,+∞)上恒成立,即m≤ 8分
(2)当m=2时,f′(x)=x =,
令f′(x)=0得x=±, 10分
当x∈[1,)时,f′(x)<0,当x∈(,e)时,f′(x)>0,
故x=是函数f(x)在[1,e]上唯一的极小值点,故f(x)min=f()=1 ln2,
又f(1)=,f(e)=e2 2=>,故f(x)max= 14分
