解：（1）当a＝－2时， f ′(x)＝3x2－6 ．

令 f ′(x)＝0 得x＝，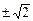

故当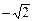 x＜或x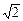＞时， f ′(x) ＞0 ，f(x) 单调递增；

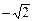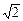当＜x＜时， f ′(x)＜0， f(x) 单调递减．

所以函数f(x)的单调递增区间为 (－∞，]，[，＋∞)，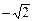

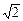单调递减区间为 (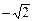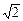，)． …………………………………………3分

（2）解法一：因＝3x2＋3a，

故g(x) ＝3x2－ax＋3a－3．

令g(x)＝h(a)＝a(3－x)＋3x2－3，

要使 h(a)＜0对满足－1≤a≤1的一切 a成立，则

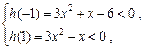0＜x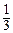＜． …………………………………… 7分

解法二：f ′(x)＝3x2＋3a，

故g(x)＝3x2－ax＋3a－3．

由g(x)＜0可解得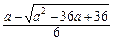＜x＜．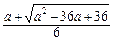

因为＝a2－36a＋36在[－1，1]单调递减，

因此 h1(a)＝在[－1，1] 单调递增，故h1(a)≤h1(1) ＝0

设h2(a)＝，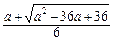

则h′2(a)＝，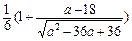

因为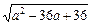≥1，

所以 h′2(a)≤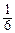(1＋a－18)＜0，

从而h2(a) 在[－1，1] 单调递减，

故h2(a)≥h2(1)＝．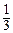

因此[h1(a)]max＜x＜[h2(a)]min，即0＜x＜．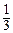

（3）因为g′(x)＝6x－a，所以 x(6x－a)＋lnx＞0，

即 a＜6x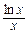＋＝h(x) 对于一切x≥2恒成立．

h′(x)＝6＋＝，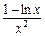

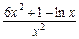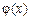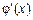令6x2＋1－lnx＝，则＝12x－．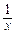

因为x≥2，所以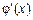＞0，

故在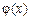[2，＋∞) 单调递增，有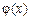≥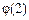＝25－ln2＞0．

因此h′(x)＞0，从而h(x)≥h(2)＝12＋．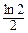

所以a＜hmin(x)＝h(2)＝12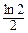＋．……………………………………12分