答案：D

欲切线与坐标轴所围成的三角形的面积，只须求出切线在坐标轴上的截距即可，故先利用导数求出在x=2处的导函数值，再结合导数的几何意义即可求出切线的斜率．最后求出切线的方程，从而问题解决．

解析：依题意得y′=e^x，

因此曲线y=e^x在点A（2，e²）处的切线的斜率等于e²，

相应的切线方程是y-e²=e²（x-2），

当x=0时，y=-e²

即y=0时，x=1，

∴切线与坐标轴所围成的三角形的面积为：

S=1/2×e²×1=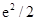

故选D．