问题
解答题
甲、乙两人都准备于下午12:00-13:00之间到某车站乘某路公交车外出,设在12:00-13:00之间有四班该路公交车开出,已知开车时间分别为12:20;12:30;12:40;13:00,分别求他们在下述情况下坐同一班车的概率.
(1)他们各自选择乘坐每一班车是等可能的;
(2)他们各自到达车站的时刻是等可能的(有车就乘).
答案
(1)他们乘车总的可能结果数为4×4=16种,
乘同一班车的可能结果数为4种,
由古典概型知甲乙乘同一班车的概率为P=
=4 16 1 4
(2)利用几何概型,设甲到达时刻为x,乙到达时刻为y,
可得0≤x≤60,0≤y≤60
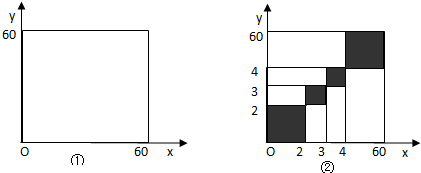
试验总结果构成区域为图①,
乘坐同一班车的事件所构成的区域为图②中4个黑色小方格,
故所求概率为P=
=20×20+10×10+10×10+20×20 60×60 5 18