问题
解答题
（本题满分10分）
已知x＝3是函数f(x)＝alnx＋x2－10x的一个极值点．
(1)求实数a；
(2)求函数f(x)的单调区间．
答案
(1) a＝12；(2) f(x)的单调减区间是(2,3)
(1)根据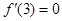
建立关于a的方程，求出a的值.
（2）根据导数大（小）于零，分别求出f(x)的单调增（减）区间.
第Ⅱ卷（共6题，50分）
解：(1)因为f′(x)＝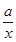
＋2
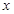－10，
所以f′(3)＝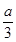
＋6－10＝0，因此a＝12 …………3分
(2)由(1)知，f(x)＝12lnx＋x2－10x，x∈(0，＋∞)
f′(x)＝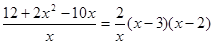
………………6分
当f′(x)>0时，x∈(0,2)∪(3，＋∞)，，
当f′(x)<0时，x∈(2,3) …………8分
所以f(x)的单调增区间是(0,2)，(3，＋∞)
f(x)的单调减区间是(2,3)． …………10分
