问题
解答题
(本题满分12分)
从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度x与底面正方形的边长的比不超过常数t.
问:(1)求长方体的容积V关于x的函数表达式;(2)x取何值时,长方体的容积V有最大值?
答案
(1)长方体的容积 ,由
,由 ,得
,得 ,-----4分
,-----4分
(2)由均值不等式知
 ,
,
当 ,即
,即 时等号成立。 --------------------6分
时等号成立。 --------------------6分
(1)当 ,即
,即 ,
, ;--------------------8分
;--------------------8分
(2)当 ,即
,即 时,
时, ,则
,则 在
在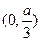 上单调递减,
上单调递减,
 ,
, 在
在 单调递增,
单调递增, --------------------11分
--------------------11分
 若
若 ,则当
,则当 时,
时, ;若
;若 ,则当
,则当 时,
时, 。--12分
。--12分
