问题
解答题
假设大王家订了一份报纸,送报人可能在早上6点-8点之间把报纸送到他家,他每天离家外出的时间在早上6点-9点之间.
(1)他离家前看不到报纸(称事件A)的概率是多少?(必须有过程、区域)
(2)请你设计一种用产生随机数模拟的方法近似计算事件A的概率.
答案
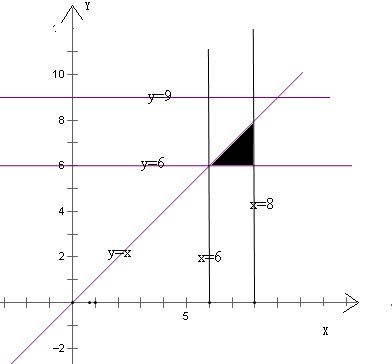
(1)如图,设送报人到达的时间为x,大王离家去工作的时间为y.(x,y)可以看成平面中的点,试验的全部结果所构成的区域为Ω={(x,y)|6≤x≤8,6≤y≤9} 是一个矩形区域,事件A表示大王离家前不能看到报纸,所构成的区域为A={(x,y)∈Ω|x≥y},
又SΩ=6SA=
×2×2=2.这是一个几何概型,1 2
所以P(A)=SA SΩ
=2 6
.1 3
即大王离家前不能看到报纸的概率是
.1 3
(2)
用计算机产生随机数摸拟试验,X是0~1之间的均匀随机数,Y也是0~1之间的均匀随机数,各产生N个.依序计算,如果满足(2X+6)>(3y+6),即2X-3Y>0,
那大王离家前能看到报纸,统计共有多少个,记为M,
则即P(A)≈
为估计的概率.M N