问题
选择题
设等差数列{an}的前n项和为Sn，已知(a5－1)3＋2 011·(a5－1)＝1，(a2 007－1)3＋2 011(a2 007－1)＝－1，则下列结论正确的是( )
A．S2 011＝2 011，a2 007<a5
B．S2 011＝2 011，a2 007>a5
C．S2 011＝－2 011，a2 007≤a5
D．S2 011＝－2 011，a2 007≥a5
答案
答案：A
题目分析：令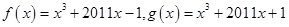
，
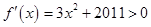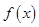在R上单调递增且连续的函数
所以函数
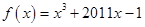只有唯一的零点
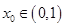，从而可得
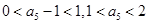，同理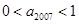
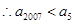
∵(a5－1)3＋2 011·(a5－1)＝1，(a2 007－1)3＋2 011(a2 007－1)＝－1两式相加整理可得，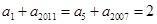
由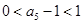
，
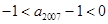可得
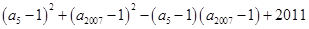＞0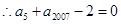
，由等差数列的性质可得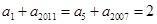
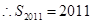
点评：本题的入手点在于通过已知条件的两数列关系式构造两函数，借助于函数单调性得到数列中某些特定项的范围，再结合等差数列中的相关性质即可求解，本题难度很大