问题
解答题
| 现有一条长度为1的绳子. (1)用剪刀剪成两段,使得两段长度都大于
(2)用剪刀剪成三段,使三段能构成三角形的概率是多少? |
答案
(1)若想两段长短都大于
,则只能在两个三等分点之间剪断,则其概率为1 3
.1 3
(2)设三段长分别为x,y,1-x-y,
则
⇒0<x<1 0<y<1 0<1-x-y<1
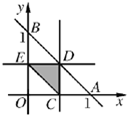
其区域构成三角形OAB(如图14-4-5).0<x<1 0<y<1 0<x+y<1
若使剪成的三段构成三角形,则x,y须满足:
⇒x+y>1-x-y y+1-x-y>x x+1-x-y>y
此时的区域为三角形CDE,故所求概率为x+y> 1 2 0<x< 1 2 0<y< 1 2
.1 4