已知函数f(x)=ax+x2-xln a(a>0,a≠1).
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调增区间;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围.
(1)y=1
(2)(0,+∞)
(3)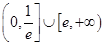
解:(1)因为函数
f(x)=ax+x2-xln a(a>0),a≠1),
所以f′(x)=ax ln a+2x-ln a,
f′(0)=0,又因为f(0)=1,
所以函数f(x)在点(0,f(0))处的切线方程为y=1.
(2)由(1)知f′(x)=axln a+2x-ln a
=2x+(ax-1)ln a.
因为当a>0,a≠1时,总有f′(x)在R上是增函数,又f′(0)=0,所以不等式f′(x)>0的解集为(0,+∞),故函数f(x)的单调增区间为(0,+∞).
(3)因为存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1成立,而当x1,x2∈[-1,1]时,|f(x1)-f(x2)|≤f(x)max-f(x)min,所以只要f(x)max-f(x)min≥e-1即可.当x变化时,f′(x) ,f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | | 极小值 | |
所以f(x)在[-1,0]上是减函数,在[0,1]上是增函数,所以当x∈[-1,1]时,f(x)的最小值f(x)min=f(0)=1,f(x)的最大值f(x)max为f(-1)和f(1)中的最大值.
f(1)-f(-1)
=(a+1-ln a)-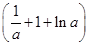
=a-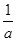 -2ln a.
-2ln a.
令g(a)=a-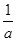 -2ln a(a>0),
-2ln a(a>0),
因为g′(a)=1+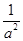 -
-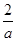 =
= 2≥0,
2≥0,
所以g(a)=a-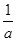 -2ln a在a∈(0,+∞)上是增函数.
-2ln a在a∈(0,+∞)上是增函数.
而g(1)=0,故当a>1时,g(a)>0,
即f(1)>f(-1);
当0<a<1时,g(a)<0,即f(1)<f(-1).
所以当a>1时,f(1)-f(0)≥e-1,即a-ln a≥e-1,易得函数y=a-ln a在a∈(1,+∞)上是增函数,解得a≥e;
当0<a<1时,f(-1)-f(0)≥e-1,
即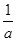 +ln a≥e-1,易得函数y=
+ln a≥e-1,易得函数y=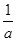 +ln a在a∈(0,1)上是减函数,解得0<a≤
+ln a在a∈(0,1)上是减函数,解得0<a≤ .
.
综上可知,实数a的取值范围为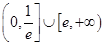 .
.