问题
问答题
设连续函数f(x)满足
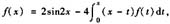
求f(x)的表达式。
答案
参考答案:题设的积分等式可改写成
[*]
在(*)式中令x=0得f(0)=0,由f(x)连续知[*]可导,从而(*)式右端各项均可导,由此f(x)必可导,将(*)式两端求导可得
[*]
在(**)式中令x=0得f’(0)=4,同样由(**)式右端各项均可导知f(x)二阶可导,且
f"(x)=-8sin2x-4f(x)
于是函数y=f(x)是二阶常系数线性微分方程初值问题
[*]
的特解
微分方程y"+4y=0对应的特征方程是λ2+4=0,其特征根为λ1=2i,λ2=-2i,根据方程右端项的形式知非齐次微分方程的特解具有形式
y*=x(Acos2x+Bsin2x),
其中A,B是待定常数,由于
(y*)"=-4x(Acos2x+Bsin2x)+4(Bcos2x-Asin2x),
为使y*是非齐次线性微分方程的特解,待定系数A,B应满足恒等式
4(Bcos2x-Asin2x)=-8sin2x,
由此可确定常数A=2,B=0,故所求非齐次微分方程的通解为
y=c1cos2x+c2sin2x+2xcos2x
由初值y(0)=0可确定常数c1=0,由于
y’=2c2cos2x+2cos2x-4xsin2x,
由初值y’(0)=4可确定常数c2=1,
故所求函数f(x)=sin2x+2xcos2x。
