问题
填空题
设P为曲线C：f(x)＝x2－x＋1上的点，曲线C在点P处的切线斜率的取值范围是[－1,3]，则点P的纵坐标的取值范围是________．
答案
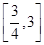
设P(x0，y0)，则f′(x)＝2x－1.
∴－1≤2x0－1≤3，即0≤x0≤2.
∵y0＝f(x0)＝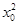
－x0＋1＝
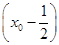2＋
，
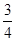∵x0∈[0,2]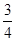，∴≤y0≤3，
故点P的纵坐标的取值范围是.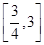
搜题请搜索小程序“爱下问搜题”
设P为曲线C：f(x)＝x2－x＋1上的点，曲线C在点P处的切线斜率的取值范围是[－1,3]，则点P的纵坐标的取值范围是________．
设P(x0，y0)，则f′(x)＝2x－1.
∴－1≤2x0－1≤3，即0≤x0≤2.
∵y0＝f(x0)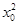＝－x0＋1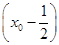＝2＋，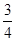
∵x0∈[0,2]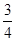，∴≤y0≤3，
故点P的纵坐标的取值范围是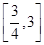.