问题
解答题
设集合A={x|
|
答案
集合A={x|
<0}={x|-3<x<3},x+3 x-3
又∵方程x2+2px-q2+1=0有两个实数根,
∴△≥0,即有:
,-3<p<3 -3<q<3 △=(2p)2-4(-q2+1)≥0
即
.-3<p<3 -3<q<3 p2+q2≥1
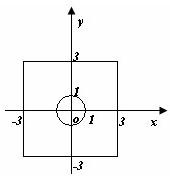
在坐标平面内画出其表示的平面区域,如图所示,是正方形内单位圆外的部分.
其中圆的面积为π,正方形的面积为36,
根据几何概率的计算公式得,
方程x2+2px-q2+1=0有两个实数根的概率:P=
=S圆外的部分 S正方形
.36-π 36