问题
解答题
求过点(2,0)且与曲线y＝x3相切的直线方程．
答案
y＝0或27x－y－54＝0
设切点坐标为(x0，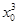
)，则由于y′＝3x2，所以切线斜率为3
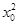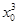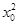，切线方程为y－＝3(x－x0)，它过点(2,0)，
∴0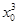－＝3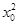(2－x0)
∴x0＝0或x0＝3.
若x0＝0，则切点坐标为(0,0)，切线方程为y＝0.
若x0＝3，则切点坐标为(3,27)，切线方程为y－27＝3×32(x－3)，即27x－y－54＝0.
所以，所求直线方程为y＝0或27x－y－54＝0
