问题
解答题
将长为L的木棒随机折成3段,求3段构成三角形的概率.
答案
设A=“3段构成三角形”,x、y分别表示其中两段的长度,则第3段的长度为L-x-y,则{Ω|(x,y)|0<x<L,0<y<L,0<x+y<L}.要使3段构成三角形,当且仅当任意2段之和大于第3段,即x+y>L-x-y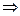 x+y>
x+y>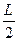 ;x+L-x-y>y
;x+L-x-y>y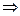 y
y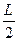 ;y+L-x-y>x
;y+L-x-y>x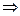 x<
x<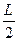 .
.
故A={(x,y)|x+y>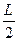 ,y<
,y<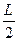 ,x<
,x<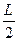 }.
}.
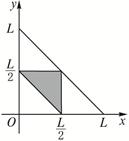
由上图可知所求概率为
P(A)=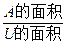 =
=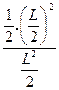 =
=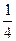 .
.
将三段长度表示出来,根据构成三角形的条件列出不等式,将问题转化为面积比的几何概型.
