问题
解答题
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
答案
设为该儿童分别预订x个单位的午餐和y个单位的晚餐,
设费用为F,则F=2.5x+4y,
由题意知约束条件为:12x+8y≥64 6x+6y≥42 6x+10y≥54 x>0,y>0
画出可行域如下图:
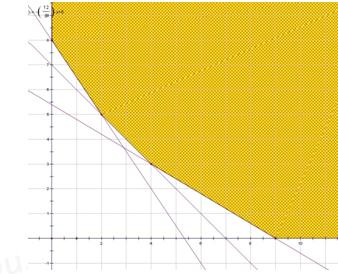
变换目标函数:y=-
x+5 8 F 4
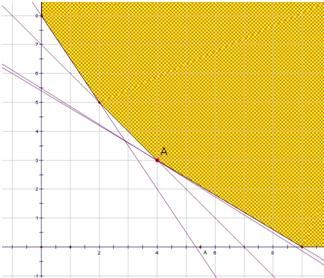
当目标函数过点A,即直线6x+6y=42与6x+10y=54的交点(4,3)时,F取得最小值.
即要满足营养要求,并且花费最少,应当为儿童分别预订4个单位的午餐和3个单位的晚餐.

