问题
解答题
盒内有大小相同的9个球，其中2个红 * * ，3个白 * * ，4个黑 * * 。规定取出1个红 * * 得1分，取出1个白 * * 得0分，取出1个黑 * * 得-1分。现从盒内任取3个球，
（1）求取出的3个球颜色互不相同的概率；
（2）求取出的3个球得分之和恰为1分的概率；
（3）设ξ为取出的3个球中白 * * 的个数，求ξ的分布列和数学期望；
（4）求取出的3个球得分之和是负分的概率。
答案
解：（1）记 “取出1个红 * * ，1个白 * * ，1个黑 * * ”为事件A，
则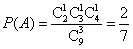
；
（2）记 “取出1个红 * * ，2个白 * * ”为事件B，“取出2个红 * * ，1个黑 * * ”为事件C，
则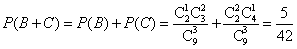
；
（3）ξ可能的取值为0，1，2，3，
，
，
，
，
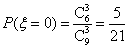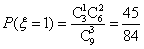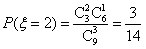ξ的分布列为：
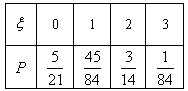
ξ的数学期望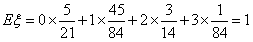
。
（4）记“取出3个黑 * * ”为事件D，“取出2个黑 * * ，1个白 * * ”为事件E，
“取出2个黑 * * ，1个红 * * ”为事件F，“取出1个黑 * * ，2个白 * * ”为事件G，
=
。
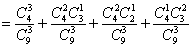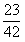红官不禁，尽教飞舞出宫墙。