问题
问答题
已知矩阵
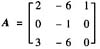 和
和
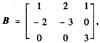
试判断矩阵A和B是否相似,若相似则求出可逆矩阵P,使P-1AP=B,若不相似则说明理由。
答案
参考答案:由矩阵A的特征多项式
[*]
得到矩阵A的特征值是 λ1=3,λ2=λ3=-1。
由矩阵B的特征多项式
[*]
得到矩阵B的特征值也是 λ1=3,λ2=λ3=-1。
当λ=-1时,由秩
[*]
知(-E-A)x=0有2个线性无关的解,即λ=-1时矩阵A有2个线性无关的特征向量,矩阵A可以相似对角化。
而(-E-B)x=0只有1个线性无关的解,即λ=-1时矩阵B只有1个线性无关的特征向量,矩阵曰不能相似对角化,因此矩阵A和B不相似。
解析:[*]
