问题
解答题
阅读理解我们知道：多项式a2+6a+9可以写成（a+3）2的形式，这就是将多项式a2+6a+9因式分解．当一个多项式（如a2+6a+8）不能写成两数和（或差）的平方的形式时，我们通常采用下面的方法：a2+6a+8=（a+3）2﹣1=（a+2）（a+4）．请仿照上面的方法，将下列各式因式分解：
（1）x2﹣6x﹣27；
（2）a2+3a﹣28；
（3）x2﹣（2n+1）x+n2+n．
答案
解：（1）x2﹣6x﹣27，
=x2﹣6x+9﹣36，
=（x﹣3）2﹣62，
=（x﹣3﹣6）（x﹣3+6），
=（x+3）（x﹣9）
=（x+3)2(x-3)；
（2）a2+3a﹣28，
=a2+3a+（
）2﹣（
）2﹣28，
=（a+
）2﹣
，
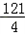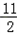=（a+
﹣
）（a+
+
），
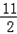=（a﹣4）（a+7）；
（3）x2﹣（2n+1）x+n2+n，
=x2﹣（2n+1）x+（n+
）2﹣（n+
）2+n2+n，
=（x﹣n﹣
）2﹣（
）2，
=（x﹣n﹣
﹣
）（x﹣n
+
），
=（x﹣n﹣1）（x﹣n）．