阅读下文,完成后面的题目。(9分)
左师触龙言愿见太后。左师公曰:“老臣贱息舒祺,最少,不肖。而臣衰,窃爱怜之。愿令得补黑衣之数,以卫王宫。没死以闻。”太后曰:“敬诺。年几何矣?”对曰:“十五岁矣。虽少,愿及未填沟壑而托之。”太后曰:“丈夫亦爱怜其少子乎?”对曰:“甚于妇人。”太后笑曰:“妇人异甚。”对曰:“老臣窃以为媪之爱燕后贤于长安君。”曰:“君过矣,不若长安君之甚。”左师公曰:“父母之爱子,则为之计深远。媪之送燕后也,持其踵为之泣,念悲其远也,亦哀之矣。已行,非弗思也,祭祀必祝之,祝曰:‘必勿使反!’岂非计久长,有子孙相继为王也哉?”太后曰:“然。”
左师公曰:“今三世以前,至于赵之为赵,赵王之子孙侯者,其继有在者乎?”曰:“无有。”曰:“微独赵,诸侯有在者乎?”曰:“老妇不闻也。”“此其近者祸及身,远者及其子孙。岂人主之子孙则必不善哉?位尊而无功,奉厚而无劳,而挟重器多也。今媪尊长安君之位,而封之以膏腴之地,多予之重器,而不及今令有功于国。一旦山陵崩,长安君何以自托于赵?老臣以媪为长安君计短也,故以为其爱不若燕后。”太后曰:“诺。恣君之所使之。”于是为长安君约车百乘质于齐,齐兵乃出。
小题1:对下列句中加点的词的意思判断正确的一项是( )
①臣衰,窃爱怜之 ②老臣窃以为媪之爱燕后贤于长安君
③丈夫亦爱怜其少子乎? ④父母爱子,则为之计深远
A.两个“窃”字的意思相同,两个“子”字的意思也相同。
B.两个“窃”字的意思不同,两个“子”字的意思也不同。
C.两个“窃”字的意思相同,两个“子”字的意思不同。
D.两个“窃”字的意思不同,两个“子”字的意思相同。小题2:对下列句中“之”的意义和用法,判断正确的一项是( )
①窃爱怜之 ②父母之爱子 ③持其踵为之泣 ④祭祀必祝之
A.①②句相同,③④句不同。
B.①②句不同,③④句相同。
C.①②句不同,③④句也不同。
D.①②句相同,③④句也相同。小题3:与选文内容不符的一项是( )
A.左师公请求太后,让其少子补黑衣之数,其目的是以此为话题,委婉劝谏太后。
B.左师触龙私下里认为赵太后爱燕后不如爱长安君。
C.左师触龙认为,为子女作长远打算才是真正地爱护自己的子女。
D.燕后远嫁,赵后思念她,每次祭祀时,赵后必为她祈祷,保佑她不被送回来。左师认为这才是真正为子女作长远打算。小题4:翻译下列文言句子(8 分)
(1)吾不能早用子,今急而求子,是寡人之过也。
译:___________________________________________________________________________
(2)夫晋,何厌之有?
译:___________________________________________________________________________
(3)一旦山陵崩,长安君何以自托于赵?
译:___________________________________________________________________________
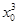 +1.
+1.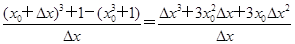 =Δx2+3x0Δx+3
=Δx2+3x0Δx+3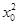 .
.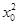 ,切线的斜率为k=3
,切线的斜率为k=3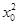 .
.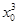 +1)=3
+1)=3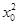 (1-x0).∴x0=1或x0=-
(1-x0).∴x0=1或x0=-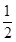 .
.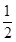 时,切线方程为3x-4y+5=0.
时,切线方程为3x-4y+5=0.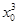 +1.
+1.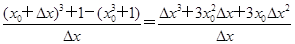 =Δx2+3x0Δx+3
=Δx2+3x0Δx+3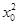 .
.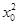 ,切线的斜率为k=3
,切线的斜率为k=3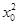 .
.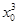 +1)=3
+1)=3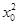 (1-x0).∴x0=1或x0=-
(1-x0).∴x0=1或x0=-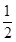 .
.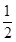 时,切线方程为3x-4y+5=0.
时,切线方程为3x-4y+5=0.