问题
解答题
求过曲线y＝ex上的点P(1，e)且与曲线在该点处的切线垂直的直线方程．
答案
x＋ey－e2－1＝0
y′＝ex，∴曲线在点P处的切线的斜率为e1＝e.
∴过P点与曲线在点P处的切线垂直的直线的斜率为－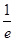
.
∴所求方程为y－e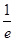＝－ (x－1)，即x＋ey－e2－1＝0.
搜题请搜索小程序“爱下问搜题”
求过曲线y＝ex上的点P(1，e)且与曲线在该点处的切线垂直的直线方程．
x＋ey－e2－1＝0
y′＝ex，∴曲线在点P处的切线的斜率为e1＝e.
∴过P点与曲线在点P处的切线垂直的直线的斜率为－.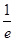
∴所求方程为y－e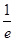＝－ (x－1)，即x＋ey－e2－1＝0.