问题
解答题
求抛物线y＝x2上点到直线x－y－2＝0的最短距离．
答案
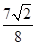
由题意得，与直线x－y－2＝0平行的抛物线y＝x2的切线对应的切点到直线x－y－2＝0距离最短，设切点为(x0，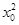
)，则切线的斜率为2x0＝1，所以x0＝
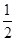，切点为
，切点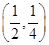到直线x－y－2＝0的距离为d＝
搜题请搜索小程序“爱下问搜题”
求抛物线y＝x2上点到直线x－y－2＝0的最短距离．
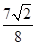
由题意得，与直线x－y－2＝0平行的抛物线y＝x2的切线对应的切点到直线x－y－2＝0距离最短，设切点为(x0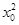，)，则切线的斜率为2x0＝1，所以x0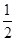＝，切点为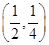，切点到直线x－y－2＝0的距离为d＝