问题
解答题
已知二次函数y=f1（x）的图象以原点为顶点且过点（1，1），反比例函数y=f2（x）的图象与直线y=x的两个交点间距离为8，f（x）=f1（x）+f2（x）。
（1）求函数f（x）的表达式；
（2）证明：当a>3时，关于x的方程f（x）=f（a）有三个实数解。
答案
解：（1）由已知，设f1（x）=ax2，
由f1（1）=1，得a=1，
∴f1（x）= x2
设f2（x）=
（k>0），
它的图象与直线y=x的交点分别为A（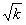
，
）B（-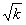
，-）
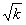由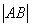
=8，得k=8
∴f2（x）=
故f（x）=x2+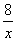
。
（2）f（x）=f（a），得x2+
=a2+
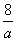， 即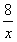
=-x2+a2+
在同一坐标系内作出f2（x）=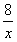
和f3（x）=-x2+a2+
的大致图象，
其中f2（x）的图象是以坐标轴为渐近线，且位于第一、三象限的双曲线，
f3（x）与的图象是以（0，a2+）为顶点，开口向下的抛物线
因此，f2（x）与f3（x）的图象在第三象限有一个交点，即f（x）=f（a）有一个负数解
又∵f2（2）=4，f3（2）= -4+a2+
当a>3时，f3（2）-f2（2）=a2+-8>0，
∴当a>3时，在第一象限f3（x）的图象上存在一点（2，f（2））在f2（x）图象的上方
∴f2（x）与f3（x）的图象在第一象限有两个交点，即f（x）=f（a）有两个正数解
因此，方程f（x）=f（a）有三个实数解。