问题
解答题
已知:抛物线y=a(x-2)2+b(ab<0)的顶点为A,与x轴的交点为B,C(点B在点C的左侧)。
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由。
答案
解:(1)抛物线对称轴方程:x=2;
(2)设直线x=2与x轴交于点E,则E(2,0),
∵抛物线经过原点,
∴B(0,0),C(4,0)
∵△ABC为直角三角形,根据抛物线的对称性可知AB=AC,
∴AE=BE=EC,
∴A(2,-2)或(2,2),
当抛物线的顶点为A(2,-2)时, ,
,
把(0,0)代入,得: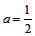 ,此时b=-2,
,此时b=-2,
当抛物线的顶点为A(2,2)时,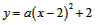 ,
,
把(0,0)代入,得: ,此时b=2,
,此时b=2,
∴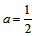 ,b=-2或,
,b=-2或,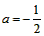 ,b=2;
,b=2;
(3)依题意,B、C关于点E中心对称,
当A,D也关于点E对称,且BE=AE时, 四边形ABDC是正方形,
∵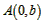 ,
,
∴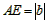 ,
,
∴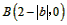 ,
,
把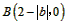 代入
代入 ,得ab2+b=0,
,得ab2+b=0,
∵b≠0,
∴ab=-1。

