问题
解答题
已知二次函数y=x2+bx-3的图象经过点P（-2，5）。
（1）求b的值并写出当1＜x≤3时y的取值范围；
（2）设P1（m，y1）、P（m+1，y2）、P（m+2，y3）在这个二次函数的图象上，
①当m=4时，y1，y2，y3能否作为同一个三角形三边的长？请说明理由；
②当m取不小于5的任意实数时，y1，y2，y3一定能作为同一个三角形三边的长，请说明理由。
答案
解：（1）由题意得：4-2b-3=5
∴b=-2
则y=x2-2x-3=（x-1）2-4
∴当1＜x≤3时，-4＜y≤0；
（2）y1= m2-2m-3
y2= （m+1）2-2（m+1）-3=m2-4
y3= （m+2）2-2（m+2）-3= m2+2m-3
① 当m=4时，y1=5，y2=12，y3=21
∵5+12＜21
∴
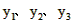不能作为同一个三角形三边的长；
②当m≥5时，
∵m＜m+1＜m+2，
而函数当x≥1时y随x增大而增大
∴y1＜y2＜y3
y1+y2- y3= （m2-2m-3）+ （m2-4）- （m2+2m-3）=m2-4m-4=（m-2）2-8≥1＞0
∴
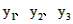一定能作为同一个三角形三边的长。