问题
填空题
设命题p：
|
答案
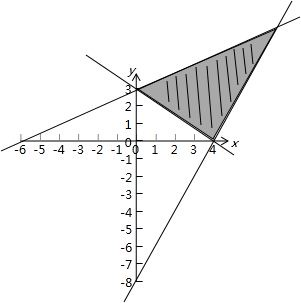
p所对应的区域为，
q对应的区域为以原点为圆心以r为半径的圆．
又在q对应区域内的点一定在p对应的区域外部，
在p对应区域外部的点一定不在q对应的区域内部．
所以当圆与直线3x+4y-12=0相切时，半径r最大，
此时r=
=|0+0-12| 32+42
．12 5
故答案为：12 5
搜题请搜索小程序“爱下问搜题”
设命题p：
|
p所对应的区域为，
q对应的区域为以原点为圆心以r为半径的圆．
又在q对应区域内的点一定在p对应的区域外部，
在p对应区域外部的点一定不在q对应的区域内部．
所以当圆与直线3x+4y-12=0相切时，半径r最大，
此时r=
=|0+0-12| 32+42
．12 5
故答案为：12 5