问题
填空题
记定义在R上的函数y＝f(x)的导函数为f′(x)．如果存在x0∈[a，b]，使得f(b)－f(a)＝f′(x0)(b－a)成立，则称x0为函数f(x)在区间[a，b]上的“中值点”．那么函数f(x)＝x3－3x在区间[－2,2]上“中值点”的个数为________．
答案
2
设函数f(x)的“中值点”为x0，则f′(x0)＝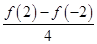
＝
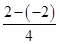＝1，即3x02－3＝1，解得x0＝±
＝±
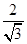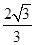∈[－2,2]，故函数y＝x3－3x在区间[－2,2]上“中值点”的个数是2．