问题
解答题
已知函数f(x)＝x3＋ax2＋bx＋a2(a，b∈R)．
(1)若函数f(x)在x＝1处有极值10，求b的值；
(2)若对于任意的a∈[－4，＋∞)，f(x)在x∈[0,2]上单调递增，求b的最小值．
答案
（1）b＝－11 （2）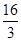
解：(1)f′(x)＝3x2＋2ax＋b，
于是，根据题设有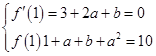
，
解得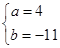
或
.
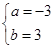当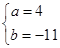时，f′(x)＝3x2＋8x－11，Δ＝64＋132>0，所以函数有极值点；
当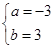时，f′(x)＝3(x－1)2≥0，所以函数无极值点．
所以b＝－11.
(2)由题意知f′(x)＝3x2＋2ax＋b≥0对任意的a∈[－4，＋∞)，x∈[0,2]都成立，
所以F(a)＝2xa＋3x2＋b≥0对任意的a∈[－4，＋∞)，x∈[0,2]都成立．
因为x≥0，
所以F(a)在a∈[－4，＋∞)上为单调递增函数或为常数函数，
①当F(a)为常数函数时，F(a)＝b≥0；
②当F(a)为增函数时，F(a)min＝F(－4)＝－8x＋3x2＋b≥0，
即b≥(－3x2＋8x)max对任意x∈[0,2]都成立，
又－3x2＋8x＝－3(x－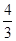
)2＋≤，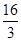
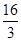所以当x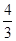＝时，(－3x2＋8x)max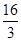＝，所以b≥.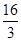
所以b的最小值为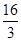.