问题
填空题
动点P（a，b）在不等式组
|
答案
w=
=a+b-3 a-1
=1+a-1+b-2 a-1
，b-2 a-1
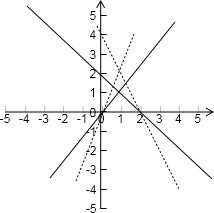
作出可行域，分析可得：
点（a，b）与点（1，2）确定的直线的斜率为（-∞，-2]∪[2，+∞），
从而可以求得w的取值范围为（-∞，-1]∪[3，+∞）；
故答案为（-∞，-1]∪[3，+∞）．
搜题请搜索小程序“爱下问搜题”
动点P（a，b）在不等式组
|
w=
=a+b-3 a-1
=1+a-1+b-2 a-1
，b-2 a-1
作出可行域，分析可得：
点（a，b）与点（1，2）确定的直线的斜率为（-∞，-2]∪[2，+∞），
从而可以求得w的取值范围为（-∞，-1]∪[3，+∞）；
故答案为（-∞，-1]∪[3，+∞）．