问题
解答题
已知抛物线y=x2+（1-2a）x+a2（a≠0）与x轴交于两点A（x1，0）、B（x2，0）（x1≠x2）。
（1）求a的取值范围，并证明A、B两点都在原点O的左侧；
（2）若抛物线与y轴交于点C，是否存在这样的a使得OA2+OB2=OA+OB+OC-1成立，若存在，求出a，若不存在，说明理由。
答案
解：（1）∵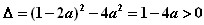
∴
∵
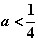
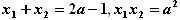
又∵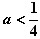
且a≠0
∴
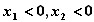
∴A、B两点都在原点O的左侧。
（2）∵
∴
∵
∴
∵
∴
∴
∴
∴
∵
∴
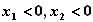
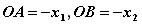
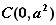
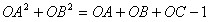
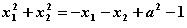
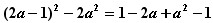
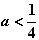
不合题意，舍去
∴不存在这样的a。