问题
问答题
如图所示，竖直长方形区域ABCD长4m，高3m，其中存在水平正交的匀强磁场和匀强电场，磁场垂直纸面向外，B=1T。匀强电场平行纸面，电场线如图中实线。一带电微粒以速度v = 5m/s从长方形区域的左下角A点沿AC方向射入其中，恰能做直线运动。
（1）判断匀强电场的方向，求出场强的大小。
（2）若在粒子射至对角线的某点时将磁场撤去，粒子恰好从长方形区域的D点射出，求撤去磁场时粒子离A点的距离。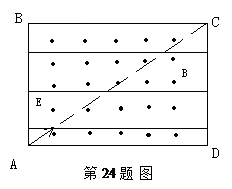
答案
（1）3v/m （2）0.1m
（1）物体做直线运动，故只能是匀速直线运动。
由图可知：此矩形的对角线和水平面的夹角为370。
因为F合="0" ，故重力、电场力、洛仑兹力只能在如图的情景下平衡。 (3分)
由左手定则，粒子带负电荷得：电场方向向左。 （2分）
电场力F=qE=Gtan370=0.75G
洛仑兹力f=qvB=G/cos370 = 1.25G
两式比较E="3v/m " （3分）
（2）撤去磁场后，粒子做类平抛运动，轨迹如图。（3分）
a = 
= 1.25g （3分）
FD = AD sin370 =" 2.4m "
FD=
at2
t=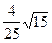
s （3分）
EF = vt=0.8
m
AE = ADcos370－EF = 3.2－0.8m =" 0.1m " （3分）