解：∵二次函数y=mx²+2x+m-4m²的图象经过原点（0，0），

∴把点（0，0）代入上面的关系式，

得0=m-4m²，

∴4m²-m=0，m（4m-1）=0，

∴m₁=0，m₂=，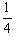

由于m=0不符合题意，应舍去，

故m=，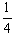

把m=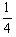代入y=mx²+2x+m-4m²，

得y=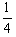x²+2x，y=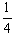（x+4）²-4，

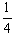∵＞0，

∴抛物线开口向上，对称轴x=-4。