问题
解答题
在1,2,3,4,5的所有排列a1,a2,a3,a4,a5中,
(Ⅰ)求满足a1<a2,a2>a3,a3<a4,a4>a5的概率;
(Ⅱ)记ξ为某一排列中满足ai=i(i=1,2,3,4,5)的个数,求ξ的分布列和数学期望。
答案
解:(Ⅰ)所有的排列种数有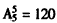 个,
个,
满足a1<a2,a2>a3,a3<a4,a4>A5的排列中,
若a1,a3,a5取集合{1,2,3}中的元素,a2,a4取集合{4,5}中的元素,都符合要求,有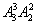 =12个;
=12个;
若a1,a3,a5取集合{l,2,4}中的元素,a2,a4取集合{3,5}中的元素,
这时符合要求的排列只有1,3,2,5,4;2,3,1,5,4;4,5,1,3,2;4,5,2,3,1共4个,
故满足a1<a2,a2>a3,a3<a4,a4>A5的概率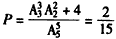 。
。
(Ⅱ)随机变量ξ可以取0,1,2,3,5,
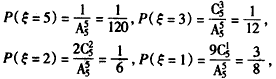
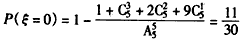 ,
,
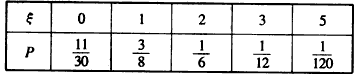
故ξ的分布列为
∴ξ的数学期望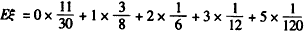 =1。
=1。