问题
解答题
袋中有8个除颜色不同其他都相同的球，其中1个为黑球，2个为白球，5个为红球．
(Ⅰ)如果从袋中一次摸出2个球，求所摸出的2个球颜色不同的概率；
(Ⅱ)如果从袋中一次摸出3个球，记得到红球的个数为X，求随机变量X的概率分布及数学期望E(X)。
答案
解：(Ⅰ)记“所摸出的2个球颜色不同”为事件A，
摸出的2个球颜色不同的摸法种数为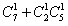
=17种，
从8个球中摸出2个球的不同摸法种数为
=28种，
所以P(A)=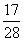
，
答：所摸出的2个球颜色不同的概率为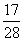
。
(Ⅱ)符合条件的摸法包括以下四种：
①3个球中没有红球，只有1种摸法；
②3个球中有1个红球，有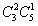
=15种不同摸法；
③3个球中有2个红球，有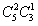
=30种不同摸法；
④3个球均为红球，有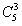
=10种不同摸法，
由题意知随机变量X的取值可以为0，l，2，3，
则随机变量X的概率分布为：
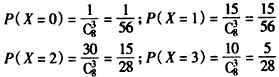
数学期望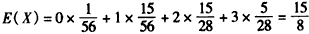
，
所以所求数学期望E(X)为
。
