问题
解答题
一个袋中装有6个形状大小完全相同的小球,球的编号分别为1,2,3,4,5,6,
(1)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;
(2)若从袋中每次随机抽取2个球,有放回的抽取3次,求恰有2次抽到6号球的概率;
(3)若一次从袋中随机抽取3个球,记球的最大编号为X,求随机变量X的分布列.
答案
解:(1)设先后两次从袋中取出球的编号为m,n,
则两次取球的编号的可能结果(m,n)共有6×6=36种,
其中编号之和为6的结果有(1,5),(5,1),(2,4),(4,2),(3,3),共有5种,
则所求概率为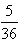 。
。
(2)每次从袋中随机抽取2个球,抽到编号为6的球的概率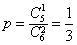 ,
,
所以,3次抽取中,恰有2次抽到6号球的概率为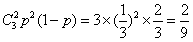 。
。
(3)随机变量X所有可能取值为3,4,5,6,
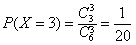 ,
,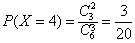 ,
,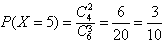 ,
,
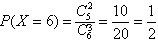 ,
,
所以,随机变量X的分布列为:
 。
。
