问题
解答题
已知:抛物线y=-x2+4x-3与x轴相交于A、B两点(A点在B点的左侧),顶点为P。
(1)求A、B、P三点坐标;
(2)在下面的直角坐标系内画出此抛物线的简图,并根据简图写出当x取何值时,函数值y大于零; (3)确定此抛物线与直线y=-2x+6公共点的个数,并说明理由。
答案
解:(1)求得A(1,0),B (3,0), P (2,1):
(2)作图正确,
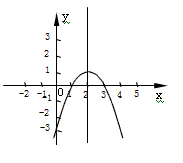
当1<x<3时,y>0;
(3)由题意列方程组得:
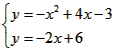
转化得:x2-6x+9=0,
△=0,
∴方程的两根相等,方程组只有一组解,
∴此抛物线与直线有唯一的公共点。
