解：（1）任取3个球的基本情况有（1，2，3），（1，2，3′），（1，2，4），（1，2，5），（1，3，3′）（1，3，4），（1，3，5），（1，3′，4），（1，3′，5），（1，4，5），（2，3，3′），（2，3，4），（2，3，5），（2，3′，4），（2，3′，5），（2，4，5），（3，3′，4），（3，3′，5），（3，4，5），（3′，4，5）共20种，

其中最大编号为4的有（1，2，4），（1，3，4），（1，3′，4），（2，3，4），（2，3′，4），（3，3′，4）共6种，

所以3个球中最大编号为4的概率为；

（2）3个球中有1个编号为3的有（1，2，3），（1，2，3′），（1，3，4），（1，3，5），（1， 3′，4），（1，3′，5），（2，3，4），（2，3，5），（2，3′，4），（2，3′，5），（3，4，5），（3′，4，5）共12种，

有2个编号为3的有（1，3，3′），（2，3，3′），（3，3′，4），（3，3′，5）共4种，

所以3个球中至少有个编号为3的概率是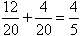。